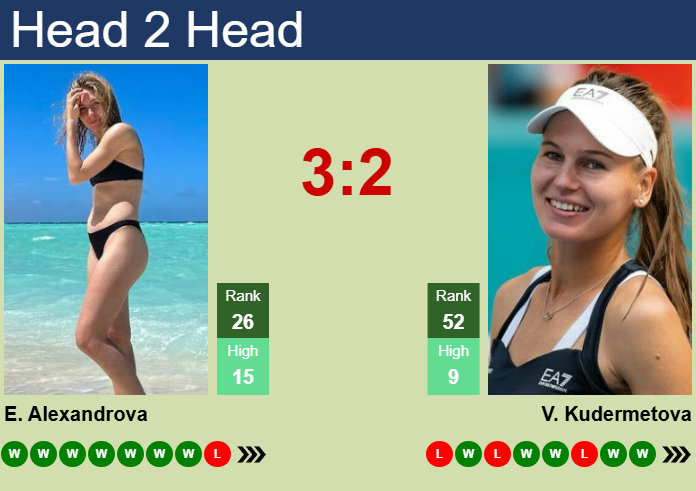
Alright, let me tell you about this tennis match I was messing around with – Azarenka vs. Kudermetova. I wasn’t betting or anything, just trying something new with data.

It all started when I stumbled upon some free tennis data. Figured, “Hey, why not see if I can predict the outcome using some basic stats?” I mean, I’m no expert, but data is data, right?
First thing I did was grab the data. I found this CSV file with match stats – things like aces, double faults, first serve percentage, all that jazz. It was messy, as data usually is, so I had to clean it up a bit.
- Removed some rows with missing data. Ain’t nobody got time for that.
- Converted some string columns to numbers – you know, making sure everything was apples to apples.
Okay, data’s clean(ish). Now what? I decided to focus on a few key stats that I thought might actually matter. Things like:
- First serve percentage.
- Break points converted.
- Total points won.
Then I started playing around with simple calculations. I created some new columns based on these stats, like the difference in first serve percentage between the two players, the ratio of break points converted, stuff like that.
After that, I tried a super basic model in Python using scikit-learn. Nothing fancy, just a Logistic Regression model. I split the data into training and testing sets, trained the model on the training data, and then made predictions on the testing data.
The results? Well, let’s just say it wasn’t perfect. I think I got like 60% accuracy or something. Not great, not terrible. I mean, it’s better than flipping a coin, but not by much.
I messed around with different features and different models – tried a Support Vector Machine (SVM) for a bit, but it didn’t really improve things. The biggest issue I think was just the limited data I had. More data, more better, right?
So, what did I learn? Well, predicting tennis matches is harder than it looks! But it was a fun little project to mess around with. I got a little more familiar with data cleaning and basic machine learning techniques. Maybe I’ll try again with a bigger dataset and some fancier models someday. Who knows? For now, it’s back to the grind!